Self-similarity in geometry is the idea of repeating a similar shape (often at a different scale) over and over again. In other words, a self-similar image contains copies of itself at smaller and smaller scales, such as the image below of the word “zoom.”

Self-similarity is a rich mathematical idea and connects to other powerful concepts such as infinity, iteration, fractals, recursion and so on. As it turns out self-similarity is also a rich source of ambigrams. This is why the third article in the series Of Art & Math is devoted to Self-Similarity. This series written with my friend Gaurav Bhatnagar is published by At Right Angles (a mathematics education magazine).

I think this is easily the best article of the three we have written so far. It has some of the best original designs I have created. Gaurav pushed me hard mathematically, and I dare say, I met the challenge (at least part of the way). I don’t want to reveal too many of the designs in the article (links to download the article are given below) but here are a couple. Below are two different designs for the word “Infinity.”
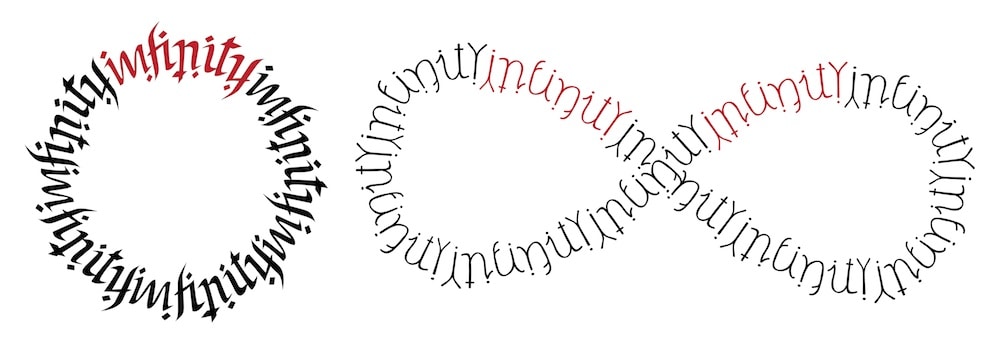
These two different ambigram designs for “infinity” are subtly different from each other. In both cases the word can be read even when you rotate the design around – both at the top of the circle and the bottom! Notice how in the first design the chain is created by “in” mapping to itself and “finity” mapping to itself. In contrast the second design breaks the word up differently, mapping “ity” to “in” and “fin” to itself. In addition the first design wraps around a circle – for ever and ever and the second says infinity both in words and in symbol!
The idea of infinity is captured somewhat differently in the next two images.

The first focuses on mapping the design onto a sphere while the second is a self-similar shape that circles inwards forever. In either case the design can be interpreted in two different ways. Either being made of an infinite repetition of the word “finite” or the infinite repetition of the word “infinite” (where the shape that reads as the last “e” in the word “finite” can be read as “in” in the word “infinite” when rotated by 90 degrees).
There are lot more designs in the actual article. If you love math or ambigrams are just interested in exploring some cool ideas, go ahead click the links at the end of this post.
All in all this series seeks to reveal the hidden beauty of mathematics – and thus it is only fitting that it ends with this design for “hidden beauty.”
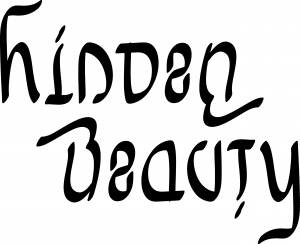
You can download each of the articles in the series Of Art & Math by following the links below
- Introducing Ambigrams: Blog post | Direct link to PDF
- Symmetry: Blog post | direct link to PDF
- Self-Similarity: Direct link to PDF
Alternatively you can download all three articles in one large(-ish) PDF by clicking here.




cool post